Focusing by Contrastive Attention: Enhancing VLMs' Visual Reasoning
Abstract
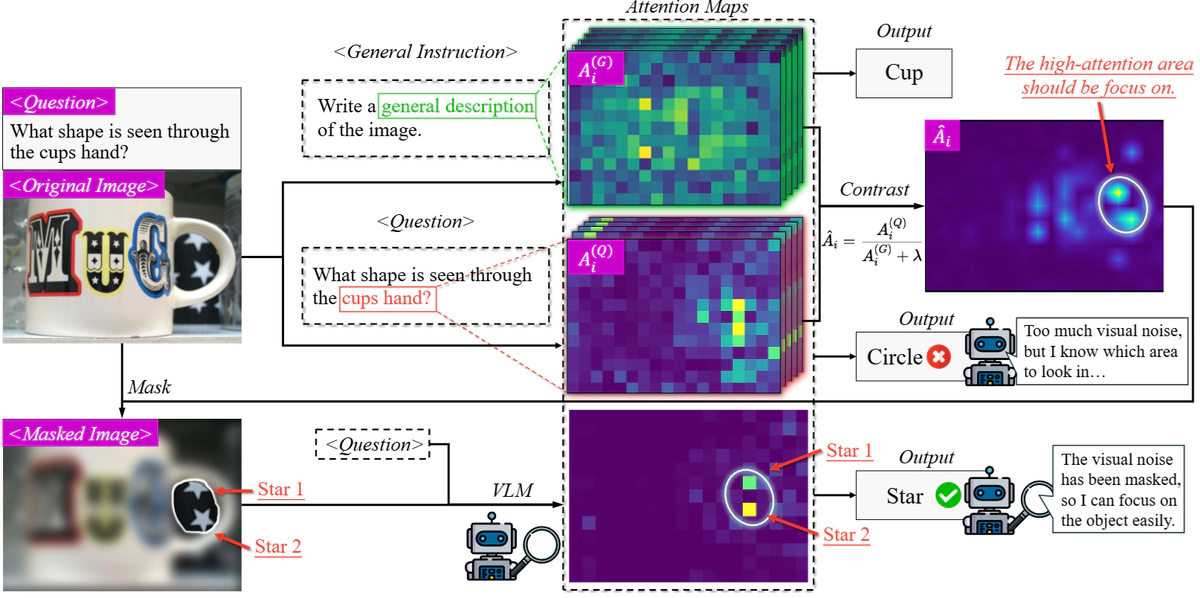
Vision-Language Models (VLMs) have demonstrated remarkable success across diverse visual tasks, yet their performance degrades in complex visual environments. While existing enhancement approaches require additional training, rely on external segmentation tools, or operate at coarse-grained levels, they overlook the innate ability within VLMs. To bridge this gap, we investigate VLMs’ attention patterns and discover that: (1) visual complexity strongly correlates with attention entropy, negatively impacting reasoning performance; (2) attention progressively refines from global scanning in shallow layers to focused convergence in deeper layers, with convergence degree determined by visual complexity. (3) Theoretically, we prove that the contrast of attention maps between general queries and task-specific queries enables the decomposition of visual signal into semantic signals and visual noise components. Building on these insights, we propose Contrastive Attention Refinement for Visual Enhancement (CARVE), a training-free method that extracts task-relevant visual signals through attention contrasting at the pixel level. Extensive experiments demonstrate that CARVE consistently enhances performance, achieving up to 75% improvement on open-source models. Our work provides critical insights into the interplay between visual complexity and attention mechanisms, offering an efficient pathway for improving visual reasoning with contrasting attention.
CARVE:无需训练,利用对比注意力让视觉模型更专注
你是否曾经在书架前寻找一本书,却因为密密麻麻的书脊而眼花缭乱?或者在超市货架前,面对琳琅满目的商品标签而一时找不到目标?其实,视觉语言模型(VLMs)也面临着同样的困扰。
本篇发现了一个有趣的现象:视觉复杂度会让AI模型的注意力"走神",就像人类在复杂场景中会分心一样。我们提出的 CARVE(Contrastive Attention Refinement for Visual Enhancement) 方法,通过对比注意力机制,帮助模型在视觉噪声中聚焦关键信息,在开源模型上实现了大幅的性能提升。
一、发现:视觉模型也会"眼花缭乱"?
研究团队首先探索了一个基础问题:复杂的视觉信息是否会像影响人类一样,干扰VLMs的注意力机制,使其难以聚焦于任务相关区域?
1.1 注意力的演化规律
通过对Qwen2.5-VL-3B-Instruct模型在TextVQA数据集上的深入分析,研究团队发现了注意力分布的层次性演化规律:
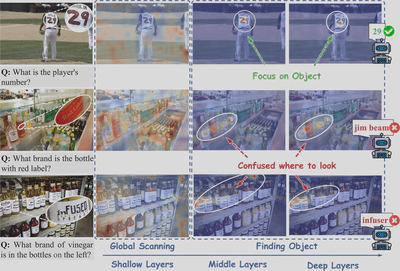
如上图所示,注意力呈现出明显的渐进式细化过程:
- 浅层(Shallow layers):进行广泛的全局扫描,注意力分布相对均匀
- 中层(Middle layers):开始区域性定位,注意力逐渐收敛
- 深层(Deep layers):实现聚焦收敛,理想情况下应锁定任务相关区域
1.2 复杂度带来的"注意力困境"
然而,视觉复杂度严重影响了这一收敛过程:
- 简单场景(第1行):目标清晰、干扰项少,高注意力区域成功收窄并对齐任务相关区域
- 复杂场景(第2-3行):纹理丰富、颜色繁杂,即使到深层,注意力权重仍然分散
正如图中标注的"Confused where to look",这种注意力分散类似于人类面对拥挤货架时的犹豫不决,最终导致推理失败。
二、量化:视觉复杂度对注意力有怎样的影响?
为了定量地研究这一现象,研究团队将视觉复杂度分解为两个纹理和颜色维度,并建立了量化指标。
纹理复杂度:对于输入图像 $\mathcal{I} \in \mathbb{R}^{H \times W \times 3}$,纹理复杂度通过Canny边缘检测定义: $$ \mathcal{T}_c(\mathcal{I}) = \frac{1}{HW} \sum_{i=1}^{H} \sum_{j=1}^{W} \mathcal{E}(\mathcal{I})_{ij} = \frac{\|\mathcal{E}(\mathcal{I})\|_1}{HW} \in [0, 1] $$
其中 $\mathcal{E}(\mathcal{I}) \in \{0,1\}^{H \times W}$ 是二值边缘图。值越高表示纹理越复杂。
颜色复杂度:通过HSV色彩空间中色相分布的Shannon熵来衡量: $$ \mathcal{C}_c(\mathcal{I}) = -\frac{1}{\ln B} \sum_{b=0}^{B-1} \rho_b \ln \rho_b, \quad \text{其中 } \rho_b = \frac{n_b}{HW}, \quad n_b = |\{(i,j) : \zeta_{ij} = b\}| $$
其中 $\rho_b = \frac{n_b}{HW}$ 是色相值为 $b$ 的像素比例, $B = 180$ 为色相区间数。

上图展示了两个样本的可视化复杂度分析:第一行显示高复杂度(密集边缘、多样色彩分布),第二行显示低复杂度(稀疏边缘、集中色相值)。
注意力熵:为了量化注意力分散程度,本文采用Shannon熵作为度量: $$ \overline{\mathcal{H}} = \frac{1}{|\mathcal{L}|} \sum_{l \in \mathcal{L}} \mathcal{H}(A_{l,t_{\text{end}}}^{(Q)}) = \frac{1}{|\mathcal{L}|} \sum_{l \in \mathcal{L}} \left(-\sum_{i=1}^{N_v} a_{l,t_{\text{end}},i} \ln a_{l,t_{\text{end}},i}\right) $$ 其中:
- $A_{l,t}^{(Q)} \in \mathbb{R}^{N_v}$ 是层 $l$、时间步 $t$ 的注意力图
- $N_v$ 是视觉token数量
- $\mathcal{L} = [L_{\text{start}}, L_{\text{end}}]$ 是考虑的层范围
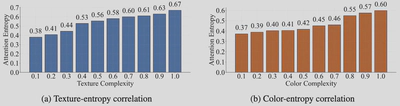
实验结果显示,纹理复杂度和颜色复杂度都与注意力熵呈现强正线性关系。这种单调趋势表明:复杂的视觉特征导致VLMs产生分散的注意力模式。
三、影响:分散的注意力如何损害性能?
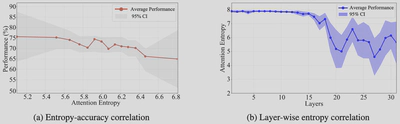
图(a)揭示了注意力熵与准确率之间的强负相关关系:当注意力熵从5.1增加到6.8时,性能从约76%下降到65%。这证实了注意力分散损害视觉推理能力。
图(b)展示了两个重要特征:
- 熵单调递减:注意力熵随层深度单调下降,与图1的观察一致
- 方差逐渐增大:95%置信区间随深度逐渐扩大,表明样本间差异性增强
这意味着:
- 对于清晰目标的样本,深层实现高度集中的注意力
- 对于噪声样本,即使在深层也保持分散的注意力模式
四、初步实验:通过手动渐进式掩盖视觉噪声
在发现视觉复杂度影响注意力进而损害性能后,一个自然的问题是:如果我们能够移除视觉噪声,是否能提升模型性能?
基于这一想法,研究团队在TextVQA数据集上进行了初步实验:首先应用渐进式掩码遮挡背景区域,然后裁剪仅保留任务相关区域,最后自适应放大到原始图像尺寸。
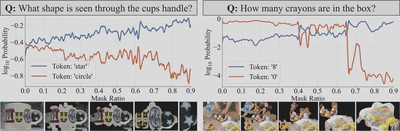
图中展示了两个代表性样本,在这两个案例中,杂乱的视觉环境最初都导致了错误预测。横轴表示掩码比例,纵轴显示候选token的对数概率( $\log_{10}$Probability)。
观察结果显示:
- 在两个样本中,错误token的概率最初都占主导地位
- 随着掩码比例的增加,正确token的概率逐渐上升
- 在掩码比例分别约为0.02和0.65时,正确token概率超过了错误token概率
这些结果提供了初步验证:掩盖视觉噪声能够提高正确token的概率。
五、理论基础:注意力分解与语义提取
在上一章节我们证明了使用掩盖视觉噪声能够提高VLM的性能,于是作者团队考虑如何将视觉噪声掩盖自动化。为此,研究团队提出了基于对比注意力的理论框架。
5.1 注意力分解
定义1(注意力分解):首先,假设VLMs的注意力分布受图像固有视觉噪声和任务相关语义信号的影响,可分解为: $$ A_{l,t}^{(Q)}(\mathcal{I}) = \mathcal{F}_{\text{vis}}(\mathcal{I}) \otimes \mathcal{F}_{\text{sem}}(Q, \mathcal{I}) $$ 其中:
- $\mathcal{F}_{\text{vis}}(\mathcal{I}) \in \mathbb{R}^{N_v}$:图像固有的视觉噪声分量
- $\mathcal{F}_{\text{sem}}(Q, \mathcal{I}) \in \mathbb{R}^{N_v}$:任务相关的语义信号分量
- $\otimes$:Hadamard积(逐元素乘积)
当使用通用指令 $G$(如"描述这张图片")时,由于缺乏特定任务来引入语义信息,语义信号函数退化为均匀分布:
$$ A_{l,t}^{(G)}(\mathcal{I}) \approx \mathcal{F}_{\text{vis}}(\mathcal{I}) \otimes \mathbf{1}_{N_v} = \mathcal{F}_{\text{vis}}(\mathcal{I}) $$5.2 语义提取优化
定义2(基于注意力分解的语义提取):为了从 $A^{(Q)}$ 中提取语义信号函数,定义估计的语义注意力 $\hat{A} \in \mathbb{R}^{N_v}_+$ 为以下优化问题的解: $$ \hat{A} = \arg\min_{\tilde{A} \in \mathcal{A}} \mathcal{J}(\tilde{A}; A^{(Q)}, A^{(G)}) $$ 目标函数基于分解构造:
$$ \mathcal{J}(\tilde{A}) = \underbrace{\sum_{i=1}^{N_v} \left( \tilde{A}_i \cdot \mathcal{F}_{\text{vis},i}(\mathcal{I}) - [\mathcal{F}_{\text{vis},i}(\mathcal{I}) \cdot \mathcal{F}_{\text{sem},i}(Q,\mathcal{I})] \right)^2}_{\text{语义重建误差}} + \underbrace{\lambda \sum_{i=1}^{N_v} \tilde{A}_i^2 \cdot \mathcal{F}_{\text{vis},i}(\mathcal{I})}_{\text{视觉抑制正则化}} $$5.3 闭式解
定理3(语义提取的闭式解):将关系式 $A^{(Q)}_i \approx \mathcal{F}_{\text{vis},i} \cdot \mathcal{F}_{\text{sem},i}$ 和 $A^{(G)}_i \approx \mathcal{F}_{\text{vis},i}$ 代入,得到: $$ \mathcal{J}(\tilde{A}) = \sum_{i=1}^{N_v} \left( \tilde{A}_i \cdot A^{(G)}_i - A^{(Q)}_i \right)^2 + \lambda \sum_{i=1}^{N_v} \tilde{A}_i^2 \cdot A^{(G)}_i $$ 求解一阶最优性条件,得到闭式解:
$$ \hat{A}_i = \frac{A^{(Q)}_i}{A^{(G)}_i + \lambda} = \frac{\mathcal{F}_{\text{vis},i} \cdot \mathcal{F}_{\text{sem},i}}{\mathcal{F}_{\text{vis},i} + \lambda} \approx \mathcal{F}_{\text{sem},i} \quad \text{当 } \mathcal{F}_{\text{vis},i} \gg \lambda $$这个公式表明,当视觉噪声占主导时( $\mathcal{F}_{\text{vis},i} \gg \lambda$),归一化能有效抑制 $\mathcal{F}_{\text{vis},i}$ 的影响,近似得到语义信号 $\mathcal{F}_{\text{sem},i}$。
六、CARVE:通过对比注意力降低视觉噪声
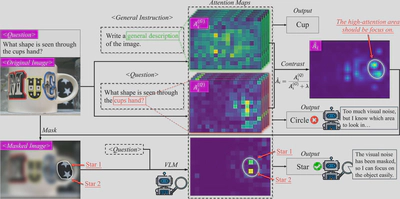
CARVE的核心思想是通过对比注意力机制来实现视觉增强。整体上需要三次推理(inference)过程来完成整个流程。
对于前两次推理,CARVE分别使用任务特定问题和通用指令来获取注意力图。
第一次推理使用原始图像 $\mathcal{I}$ 和具体问题 $Q$,通过注意力提取函数 $\Xi$ 获得任务特定注意力集合:
$$ \mathcal{A}^Q = \{A_{l,t}^{(Q)}\}_{l \in \mathcal{L}, t \in \mathcal{T}} = \Xi(\mathcal{M}, \mathcal{I}, Q) $$第二次推理使用相同的图像但配以通用指令 $G$(如"Write a general description of the image"),获得通用注意力集合:
$$ \mathcal{A}^G = \{A_{l,t}^{(G)}\}_{l \in \mathcal{L}, t \in \mathcal{T}} = \Xi(\mathcal{M}, \mathcal{I}, G) $$得到两次推理产生的注意力图之后,CARVE进行注意力对比。对所有层 $l \in \mathcal{L}$ 和时间步 $t \in \mathcal{T}$,应用对比公式:
$$ \hat{A}_{l,t} = \frac{A_{l,t}^{(Q)}}{A_{l,t}^{(G)} + \lambda} $$这一步骤通过归一化操作有效地抑制了视觉噪声的影响,提取出任务相关的语义信号。
接下来进行注意力图融合。由于不同层和时间步捕获互补信息,CARVE通过加权聚合进行融合:
$$ S = \sum_{t \in \mathcal{T}} w_t \sum_{l \in \mathcal{L}} \pi_{H \times W}(\hat{A}_{l,t}) $$其中时间步权重 $w_t = t - t_{\text{start}} + 1$,赋予后期token更大权重,因为它们包含更丰富的上下文信息。 $\pi_{H \times W}$ 函数将token维度的注意力重塑为空间维度。
融合后的注意力图 $S$ 用于生成掩码。首先计算阈值 $\tau = \mathcal{Q}_p(S)$,保留top-p百分位的像素。然后通过连通区域分析,选择累积注意力分数最高的K个区域:
$$ M^* = \bigcup_{k=1}^{K} R_k^*, \quad \text{其中} \quad R_k^* = \arg\max_{R \in \mathcal{R}} \sum_{(i,j) \in R} S(i,j) $$生成掩码后,通过视觉提取函数 $\Phi$ 对原始图像进行处理:
$$ \mathcal{I}_{\text{refined}} = \Phi(\mathcal{I}, M^*) $$函数 $\Phi$ 执行掩码、裁剪和缩放操作,移除视觉噪声并放大任务相关区域。
最后进行第三次推理,使用增强后的图像和原始问题生成最终答案:
$$ \text{Answer} = \mathcal{M}(\mathcal{I}_{\text{refined}}, Q) $$ 值得注意的是,虽然CARVE需要三次推理,但前两次推理只需要提取特定层(如20-25层)的注意力图,可以在获得所需注意力后提前终止,无需完成全部层的前向传播。此外,通用注意力图 $A^{(G)}$ 只依赖于图像而与具体问题无关,对于同一图像的多个问题可以缓存重用。这些优化使得CARVE在实际应用中的计算开销保持在可接受范围内。
七、结果
7.1 整体性能表现
研究团队在四个数据集上测试了CARVE的效果:
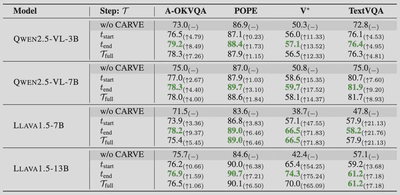
早期模型(如LLaVA系列)展现出更大的提升幅度,这表明能力有限的模型更容易受视觉复杂度干扰,因此从对比注意力引导的聚焦机制中获益更多。
7.2 时间步选择的影响
实验比较了三种时间步配置:
- $t_{\text{start}}$:使用初始生成token的注意力
- $t_{\text{end}}$:使用最终token的注意力
- $\mathcal{T}_{\text{full}}$:所有token的加权融合
结果显示性能层次: $t_{\text{end}} > \mathcal{T}_{\text{full}} > t_{\text{start}}$
这是因为后期token通过访问完整的前序序列编码了更丰富的上下文信息,其注意力图能更准确地定位目标对象。
7.3 层选择策略分析
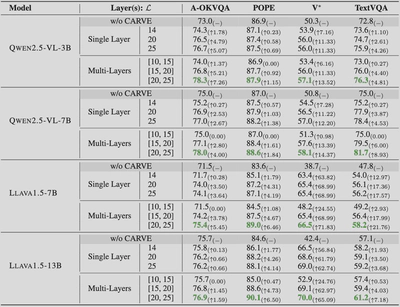
层选择实验揭示了清晰的性能排序:
- [20,25]层融合:最佳性能
- [15,20]层融合:次优
- 单层25:中等
- 单层20:较低
- [10,15]层融合:最差
以LLaVA-1.5-7B在TextVQA上的表现为例:
- [20,25]层:21.76%提升
- [15,20]层:17.99%提升
- [10,15]层:仅2.93%提升
多层融合优于单层的原因在于捕获互补信息从而具有更强的鲁棒性,而选择单层的注意力图则会有较强的随机性。
7.4 与其他方法的对比

CARVE显著优于所有基线方法:
- 外部工具(SAM、YOLO、CLIP)缺乏问题-图像上下文感知
- ViCrop虽能减少视觉噪声,但缺乏像素级噪声掩码
- CARVE在保持实用计算开销的同时达到最高准确率
八、意义与总结
此前的研究忽略了视觉语言模型的原生能力,当前方法要么需要额外训练、依赖外部分割工具,要么只能在粗粒度层面操作。而CARVE证明了通过对比通用查询和任务特定查询所生成的注意力图,就能在像素层面将视觉信号分解为语义信号和视觉噪声分量,为提高视觉语言模型的能力提供了新的思路。